미래연구소 홈페이지: https://futurelab.creatorlink.net/
*본 포스팅에 포함된 그림의 출처는 Andrew Ng 교수님의 Coursera Deep Learning specialization 과 미래연구소의 자체 제작 과제입니다.
4주차에 배운 내용들을 정리해보겠다.
-Numpy 특강3: 쉼표
Numpy만의 특별한 기능을 배웠다. 바로 slicing, indexing을 할 때 쉼표를 이용하는 것이다.
아래와 같은 배열이 있다고 하자.

여기서 아래 정사각형 꼴만을 추출하려면 어떻게 해야할까?

마음같아서는 A[5:8][5:8]를 하고 싶지만, 파이썬에서는 이렇게 할 수 없다.
왜냐하면 A[5:8]를 하는 순간

위처럼 shape가 (3,10)인 배열로 바뀌어, A[6:9]에는 6,7,8 인덱스 자체가 없기 때문에 None값을 반환한다. 대신 쉼표를 이용하여 A[5:8,5:8]를 해주면 아래와 같이 추출할 수 있다.

그렇다면 아래처럼 일부만 추출할 수도 있을까?

위 요소를 추출하려면 아래와 같은 방식으로 추출하면 된다.
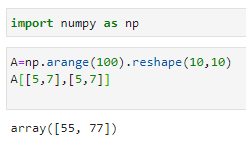
이렇게 대괄호 안에 대괄호를 넣으면 대괄호 안에 있는 숫자들이 각각 병렬적인 인덱스로 구분이 되며 이를 Fancy Indexing이라고 한다.
- Neural network의 본격적인 적용
지난주까지는 Neural network의 구조에 대해서 개략적으로만 알아봤는데, 이번 주차에서는 그것을 실제 알고리즘에 적용시켜 구현해본다. 3주차에서 다뤘던 단순 logistic regression과 가장 큰 차이점은 hidden layer에서 node의 개수가 여러개라는 점이다.

전에는 w가 (nx,1)의 shape을 가진 한줄짜리 array였지만 hidden layer의 노드를 여러 개(위 그림의 경우 4개)를 설정해주고 이를 vectorizing해서 연산을 할 수 있다.
W의 shape을 파악하는 것이 가장 중요한데, W의 shape은 (hidden layer에서 node의 개수, X의 feature 수)가 된다. $W^{[1]}$의 행 수에는 vectorizing 했던 노드의 수가 반영되고, 열 수에는 X와 곱해져야하기 때문에 feature 수가 반영된다. 이 행렬이 $b$와 더해질 때 $b$는 broadcasting되어 $W^{[1]}$의 shape으로 맞춰진다.
notation에 대해 다시 복습하자면 [] 대괄호는 layerd의 index이고 () 소괄호는 data의 index이다.
-지난주 과제에서 train accuracy는 99%였던 반면 test accuracy가 82%로 상대적으로 낮게 나왔는데, 그 점을 보완시키는 방법이 두 가지 있다.
1. Data의 수를 늘린다 : 200개 정도의 훈련 데이터는 양이 많다고 할 수 없다. 이 양을 늘려서 모델을 학습시키면 train data가 올라간다.
2. sigmoid 대신 ReLU를 쓴다.: forward propagation에서 $\hat y$를 구할 때 z를 구한후 $\sigma(z)$ 를 취했는데, 여기서 sigmoid function 대신 다른 activation function을 취하면 정확도가 올라간다. activation function은 동일한 layer에서는 동일한 것을 써야하지만, layer마다 다를 수도 있다. 후술될 과제에서는 layer가 여러 겹이기 때문에 다른 activation function을 이용해 과제를 해결한다. activation function에는 어떤 것들이 있는지 알아보자.
-Activation function의 종류

위는 sigmoid function으로 $g(z) = \frac{1}{{1 + {e^{ - z}}}}$ 이다. 치역이 0에서 1사이이기 때문에 binary classification을 할 때 강력하게 이용된다. 하지만 기울기가 0에 가까운 부분이 매우 넓다는 단점이 있다. 또 기울기의 최대값이 $\frac{1}{2}$로 작다. 기울기가 0이 되면 backward propagation에서 값이 0이되어 gradient descent를 해도 점이 이동하지 않게 되는 문제가 발생한다. 최대 기울기가 작은 점도 gradient descent에서 불리하게 작용한다.

하이퍼볼릭 탄젠트 함수를 사용할 수도 있다. tanh의 장점은 미분계수가 0인 영역이 sigmoid에 비해 적다는 점과, 최대 미분계수가 더 크다는 점이다. 그래서 sigmoid보다는 웬만하면 tanh를 쓰는 것이 정확하다고 한다.

ReLU(Rectified Linear Unit) function 은 위의 수식처럼 $g(z) = \max (0,z)$ 로 정의된다. Leaky ReLU는 미분계수가 0이 되는 것을 피하기 위하여 음수 영역에 약간의 변형을 준 것이다. ReLU가 앞선 모델과 비교해서 가지는 장점은 미분계수가 0이 되는 구간이 적다는 점이다. sigmoid나 tanh는 거의 대부분이 미분계수가 0인 반면 ReLU는 양수인 x에 대해서 강력하게 기능한다. 그리고 음수에서도 기울기가 0이 되지 않도록 변형한 것이 Leaky ReLU이다.
여기서 나는 '그렇다면 왜 y=x 같은 함수를 activation function으로 사용하지 않는걸까?'하는 물음을 가졌는데, 수업 중에 알 수 있었다. 여러 개의 layer를 쌓고 model이 '깊어진다'는 것은 결국 forward propagation 과정에서 activation function을 거칠 때 비선형함수들이 겹쳐지면서 깊어지는 것이었다. 그런데 완전히 선형인 함수를 채택하면 선형인 함수는 아무리 합성을 해도 선형이 되기 때문에 deep learning이 구현될 수가 없다는 것이었다.
-Initialization에서 유의할 점
cat classification에서는 layer가 한 개 였기 때문에 zero initialization을 해도 문제가 없었지만, layer가 2개 이상 되면 문제가 생긴다. 두 가지 문제가 생기는데, 우선 모든 원소가 0이 되면, row symmetric해지는 문제가 생긴다. 또 $W^{[l]}$이 0이 되면 $dW^{[l]}$도 0이 된다. 이 문제를 vanishing gradient라고 한다. 이를 막기 위해서 random initialization을 수행한다. np. random.randn(shape)를 이용해서 값이 겹치는 것을 막고, 적절한 상수를 곱해서 vanishing gradient를 막는다.
'Deep Learning' 카테고리의 다른 글
| CNN(Convolutional Neural Network) (0) | 2020.08.25 |
|---|---|
| [데이콘]컴퓨터 비전 학습 경진대회에 참가 결정 (0) | 2020.08.23 |
| Normalization, Standardization, Initialization, optimization (1) | 2020.08.18 |
| Softmax, One-hot encoding, Regularization, Dropout의 이해 (0) | 2020.08.15 |
| Deep Learning 미래연구소 5주차 수강후기 (0) | 2020.08.02 |
| Deep Learning 미래연구소 3주차 수강후기 (0) | 2020.07.23 |
| Deep Learning 미래연구소 2주차 수강후기 (0) | 2020.07.19 |
| Deep Learning 미래연구소 1주차 수강후기 (2) | 2020.07.10 |

